Support Vector Machines (1)

September 9, 2014 lukelushu Leave a comment

Support Vector Machines is a widely used supervised learning algorithm to learn linear and non-linear functions.

Motivation

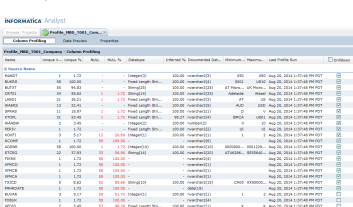
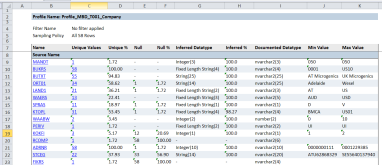
Classifying data is a common task in machine learning. Given a set of training data, each marked as belonging to one of two categories, and the goal is to decide which class a new data point will be in. In Support Vector Machines (SVM) training algorithm, a data point is viewed as a n-dimensional vector, and we want to know whether we can separate such points with a (n-1)-dimensional hyperplane, we call it a Linear Classifier. Ususally there are many hyperplanes that might classify the data. We can choose the best hyperplane as the one that represents the largest separation, or margin, between the two classes. That is, the distance from it to the nearest data point on each side is maximized. The SVM algorithm is to learn (find) such maximum-margin hyperplane or maximum-margin binary classifier.

Linear Classifiers and Margin

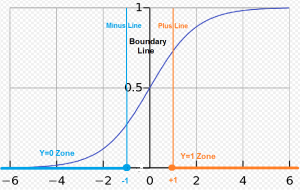
In Logistic Regression, we have the logistic regression hypothesis:

$\displaystyle h(\theta, X) = S(\theta^TX) = \frac{1}{1+e^{-\theta^TX}}$

and make the following classfication based the estimated probability:

When the probability of y =1 is greater than 0.5 then we can predict y = 1;
Else we predict y = 0.

From the property of Sigmoid function, we can get the equivalent Linear Decision Boundary or Linear Classifier is:

$\displaystyle \theta^TX=\theta_0+\theta_1x_1+\theta_1x_2 +...+ \theta_nx_n\ge 0$

Let us rewrite

$\theta^T = (\theta_0,\theta_1,\theta_2,...,\theta_n), X^T=(1, x_1, x_2, ..., x_n)$

Then the Linear Decision Boundary or Linear Classifier is

$z = \theta^TX \ge 0$

Now we can modify the Linear Classifier little bit by adding decision margins to get the SVM — We refer to SVM as a Large Margin Classifier:

If $Y = 1$ , we need $z \ge 1$ , not just $z \ge 0$
If $Y = 0$ , we need $z \le -1$ , not just $z \le 0$

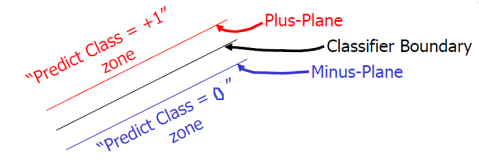
We can translate this Sigmoid function term into hyperplane language. If the training data are linearly separable, we can select two hyperplanes in a way that they separate the data and there are no points between them, and then try to maximize their distance. The region bounded by them is called “the margin”. These hyperplanes can be described by the equations

Classifier Boundary: $\{X: \theta^TX = 0\}$
Plus-Plane: $\{X: \theta^TX = +1\}$
Minus-Plane: $\{X: \theta^TX = -1\}$

Then the classification decision for a new coming example is:

Positive Class (i.e. $y=1$ ): if $\theta^TX \ge +1$
Negative Class (i.e. $y=0$ ): if $\theta^TX \le -1$

How to Calculate the Margin Width

The distance between the Plus-Plane and Minus-Plane is called the margin width. How to calculate the margin width M in terms of $\theta = (\theta_0, \theta_1,\theta_2,...,\theta_n)$ ?

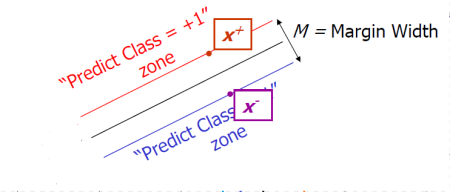
Margin

From the Classifier Boundary equation ${X: \theta^TX = 0}$ we know the vector $\theta$ is perpendicular to the Plus-Plane and Minus-Plane.

Let

$X^-$ be any point on the Minus-Plane
$X^+$ be be the closest Plus-plane-point to $X^-$ .

They are not necessarily example data points. Obviously, the vector $X^+ - X^-$ is perpendicular to the Plus-Plane and Minus-Plane, and the margin width $M = ||X^+ - X^-||$ .

Therefore, we have the following equations:

1. $\theta^TX^+ = +1$
2. $\theta^TX^- = -1$
3. $X^+ - X^- =k \theta$ (for some value k).
4. $M = ||X^+ - X^-||$

Now it is easy to calculate the margin width $M$ : Substracting the Eq. 2 from Eq. 1, we have

$\theta^T(X^+ -X^-) = 2$

and then applying the Eq.3, we get

$k \theta^T\theta = 2$

So we have

$\displaystyle k = \frac{2}{\theta^T\theta}=\frac{2}{||\theta||^2}$

Finally from Eq.4 we have

$\displaystyle M = ||X^+ - X^-|| = ||k \theta|| = k ||\theta|| =\frac{2}{||\theta||}$

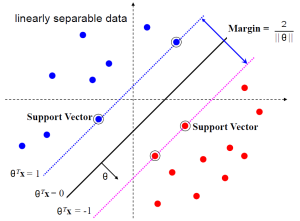
The datapoints lying on either the Minus-Plan or the Plus-Plan are called Support Vectors.

SVM – Optimization

Therefore, learning the SVM can be formulated as an optimization program: Search the $\theta$ space to find the widest margin that matches all the training example datapoints. The constraints are

$\theta^TX \ge +1$ , if $y_j = 1$
$\theta^TX \le -1$ , if $y_j = 0$

for $j=1,2,..., m$ over all the training dataset.

We can compact this constraint as

$y_j\theta^TX_j + (y_j-1)\theta^TX_j = (2y_j -1)\theta^TX_j \ge 1, j=1,2,...,m$

Equivalently, from the margin width formula above, we have the optimization problem

$\displaystyle \min_{\theta_0,\theta_1,...,\theta_n} \frac{1}{2}\sum_{i=1}^n\theta_i^2 = \frac{1}{2}||\theta||^2$

s.t. $(2y_j -1)\theta^TX_j\ge 1, j=1,2,...,m$ .

This is a quadratic optimization problem subject to linear constraints and there is a unique minimum.

QP is a well-studied class of optimization algorithms to maximize a quadratic function of some real-valued variables subject to linear constraints (linear equality and/or inequality constraints). There exist algorithms for finding such constrained quadratic optima much more efficiently and reliably than gradient ascent method.

WordPress

Tips for Writing & Editing in WordPress.com

September 5, 2014 lukelushu Leave a comment

1. How to Post Source Code — Code Snippet

Use the square bracket syntax [ code] … [ /code], NOT use the angle bracket syntax < code> … < /code>. For example,

[ code]
your code line 1
your code line 2
[ /code]

will yield

your code line 1
your code line 2

You also can use the parameter “language” or “lang” to specify how to highlight your code. See here for the details.

2. How to Write Latex and Avoid the Not Parse Error

To type a formula in WordPress type $ latex [Your LaTex code here] $. For example, $ latex \sum_{i=1}^{n}X_i$ produces $\sum_{i=1}^{n}X_i$ .

To display a formula in mat mode, type <p align=”center”> $ latex \displaystyle <Your LaTex code> $</p>.

For example <p align=”center”>$ latex \displaystyle \sum_{n=1}^\infty \frac{1}{n^2} = \frac{\pi^2}{6}. $</p> will yield

$\displaystyle \sum_{n=1}^\infty \frac{1}{n^2} = \frac{\pi^2}{6}.$

See here for the details.

Notes: If you type latex code in WordPress.com Visual editor, DO NOT insert any extra spaces between $ latex and [your code] and any extra spaces in your latex code. Otherwise, it will yield the not parse error. For example, $ latex x^2$ works fine and produce $x^2$ , but $ latex x^2$ will not work and it yields $x^2$ , since there are two spaces between $ latex and x_2 in the code. in the Text editor, it is OK to insert more spaces.

3. How to write Case function and Aligned equations?

You can use the \begin{cases} — \end{cases} to write a Case function. For example

$ latex \begin{cases}
x^2, & \text{ if } x>2 \\
1,& \text{ if } x \le 2
\end{cases}$

will yield

$\begin{cases} x^2, & \text{ if } x>2 \\ 1,& \text{ if } x \le 2 \end{cases}$

You can use the \begin{aligned} — \end{aligned} to align up the equations. Not use \begin{align*} — \end{align*}, since it will not work in WordPress.com. For example

$ latex \begin{aligned}
x &=2(a-b)+b \\
&=2a -b
\end{aligned}$

will produce

$\begin{aligned} x &=2(a-b)+b \\ &=2a -b \end{aligned}$

Data Warehouse SAP Source

Add SAP ERP Table Metadata Info into the IDQ Data Profiling Result

August 20, 2014 lukelushu 2 Comments

In data warehouse design, data profiling the data source is the first and the most important step to understand the data source. This post will show you how to get the SAP ERP metadata information and how to manually integrate this metadata information, such as Business Name, Key Flag, into the Informatica IDQ data profiling result.

Data Profiling with Informatica IDQ

Informatica Data Quality (IDQ) is a great tool you can use for the data profiling. After creating the connection to SAP ERP database (Oracle, SQl Server or others), you will able to import the SAP tables and create the Data Profiling for he tables that you are interested (see IDQ user guide for the detail). The default data profiling setting and the result will fulfill all or at least most of the data warehouse design needs. Below is an example of the data profiling result for the table T001 (Company).

You can export the the data profiling result into an excel file. The first worksheet of the excel file is named “Column Profile” and it looks like this:

Problem

Everything looks good there, except a big problem: it is not convenient to alignment up with the business names for the data analysis during the data warehouse design phrase. The SAP ERP physical table and column names is always a big headache for me to remember and mapping to their corresponding business names. We need to find a efficient way to get the SAP ERP tables and columns metadata and integrate such metadata information such as Business Name and Key Flag, into the the IDQ data profiling result. That will help us quickly understand the SAP source tables and make better decisions for data warehouse design.

SAP ERP Metadat

SAP ERP system stores the metadata information in several metadata tables. For the data profiling purpose data for warehouse design, the following metadata table will provide us all the information we need:

DD02L — SAP Tables
DD02T — SAP Table Texts
DD03L — Table Fields
DD03T — Texts for fields (language dependent)
DD04L — Data elements
DD04T — Data element texts

The following SQL queries will help us to find the table and column metadata information we need:

Table Matadata Query:

SELECT DD02L.TABNAME , DD02T.DDTEXT TAB_DESC
FROM DD02L, DD02T
WHERE DD02L.TABNAME = DD02T.TABNAME
AND DD02T.DDLANGUAGE = ‘E’
AND DD02L.TABNAME =’&&Table_Name’;

Column Matadata Query:

SELECT DD03L.TABNAME, DD02T.DDTEXT TABDESC, DD03L.FIELDNAME, DD04T.DDTEXT AS FIELDDESC, DD03L.KEYFLAG, DD03L.ROLLNAME, DD03L.POSITION, DD03L.CHECKTABLE , DD03L.NOTNULL, DD03L.DATATYPE, DD03L.LENG, DD03L.DECIMALS
FROM DD03L, DD02T, DD04T
WHERE DD04T.DDLANGUAGE = ‘E’
AND DD02T.DDLANGUAGE = ‘E’
AND DD03L.TABNAME = DD02T.TABNAME
AND DD03L.ROLLNAME = DD04T.ROLLNAME
AND DD03L.TABNAME = ‘&&Table_name’
ORDER BY DD03L.TABNAME, DD03L.POSITION;

Of course, you need to substitute the binding variable &&Table_name with the actual table name that you are interested.

Integrate the IDQ Data Profiling Result with the SAP Metadata

Since that we have the IDQ data profiling result (excel file) and the SAP metadata info from the SAP Column metadata query. We can manually integrate those two data sets together to provide a convenient way to analysis the SAP data source and make the design decision.

Metadata Integration Steps:

Open the saved IDQ data profiling result excel file.
Run the Column Matadata Query and add the query result data set (Export or Copy/Paste) into a new worksheet named “Metadata”.
In the “Metadata” worksheet, select columns FIELDNAME, FIELDDESC, KEYFLAG, CHECKTABLE, and create a new range name called “COL_METADATA” using the Excel Name Manager (see below).
Move to the first worksheet named “Column Profile”, add three (or more more if you want to add more metadata info) new columns in beginning (new columns becomes A, B and C). and add the column headers as “Business Name”, “Key Flag”, “Lookup Table” for the cells A8, B8 and C8, respectively.
Enter the following excel formula in the cells A9, B9, C9, respectively.

=VLOOKUP(D9, COL_METADATA,2,FALSE)

=VLOOKUP(D9, COL_METADATA,3,FALSE)

=VLOOKUP(D9, COL_METADATA,4,FALSE)
Verify they return the expected values. Then select the three cells A9, B9, C9 (and hold the mouse) and drag down to all the applicable rows. you will get the desired metadata information.

Machine Learning, Regression

Overfitting and Regularization

August 18, 2014 lukelushu Leave a comment

In regression or logistics regression model, fitting a linear function to the data might be too simple and lead a high bias. The higher order polynomial can provide better fitting the training set, but it may not produce a better model, since it fails to provide a general solution of applying to new examples. This is unknown as the overfitting issue.

Overfitting usually leads to very large parameter choices. To prevent the overfitting issue, we can penalize θ parameters and make some of the θ parameters really small.

Regularization

For the linear regression, with regularization, we modify the cost function and add regularized terms to shrink all the parameters ( except θ₀). That is, we can add the penalized term and the cost function becomes

$\displaystyle J(\theta) = \frac{1}{2m}\sum_{i=1}^{m}(h(\theta, X_i)-y_i)^2+\lambda\sum_{j=1}^{n}\theta_j^2$

Therefore, the regularized Gradient Descent update rule for linear regression becomes:

Simultaneously Update:

$\displaystyle \theta_0 := \theta_0 - \alpha\frac{1}{m}\sum_{i=1}^m[ h(\theta, X_i)-y_i]x_{i0}$

$\displaystyle \theta_j := \theta_j (1-\alpha \frac{\lambda}{m} ) - \alpha\frac{1}{m}\sum_{i=1}^m[ h(\theta, X_i)-y_i]x_{ij}, j= 1,2,...,n.$

where $\alpha$ is the learning rate and $\lambda$ is the regularization parameter.

The $\lambda$ should be chosen carefully – not too big. To make sure the regularized update factor $(1-\alpha \frac{\lambda}{m} )$ is often around 0.99 to 0.95. The second term is exactly the same as the original gradient descent.

For the logistic regression with the convex cost function, the regularized cost function becomes

$\displaystyle J(\theta) = \frac{1}{m}\sum_{i=1}^m [-y_i\log (h(\theta, X_i))+(1-y_i)\log (1-h(\theta,X_i))] +\lambda\sum_{j=1}^{n}\theta_j^2$

In the same way, the regularized update factor $(1-\alpha \frac{\lambda}{m} )$ is applied to the the regularized Gradient Descent update rule for logistics regression

Uncategorized

Logistic Regression

August 15, 2014 lukelushu Leave a comment

When the target variable y is a continuous value, the linear regression model can used to solve the predication problem.

When the target variable y is a discrete value. we can modify the linear regression model to develop the logistic regression algorithm to solve the Classification problems.

Binary Class Problem

The target variable y is either 1 or 0:

1 – positive class (presence)
0 – negative class (absence )

We could modify the linear regression model as the classifier by

Resealing the model output into certain range, say [0, 1].
Then setting the appropriate threshold value (say 0.5 or 0.7) for the scaled model output to assign the positive or negative class.

Logistics Hypothesis

in linear regression, we have the linear hypothesis:

$h(\theta, X) = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + ....+ \theta_n x_n = \theta^TX$ For Logistic Regression, we can resale the hypothesis

$h(\theta, X) = S (\theta^T X) : \rightarrow [0, 1]$

by applying the Sigmoid function (aka Logistic function):

$\displaystyle S(t) = \frac{1}{1+e^{-t}}$

That is,

$\displaystyle h(\theta, X) = S(\theta^TX) = \frac{1}{1+e^{-\theta^TX}}$

Since $h(\theta, X) \in [0, 1]$ , we can interpret that value as the estimated probability that y=1 on input x for the give parameters $\theta$ . That is,

$\displaystyle P(y=1|X; \theta) = h(\theta, X)$

Then we have

$\displaystyle P(y=0|X; \theta) = 1-P(y=1|X; \theta) = 1- h(\theta, X)$

and furthermore,

$\displaystyle \frac{P(y=1|X;\theta)}{P(y=0|X; \theta) } = \frac{h(\theta, X)}{1- h(\theta, X)} = e^{\theta^TX}$

That is

$\displaystyle \log\frac{P(y=1|X;\theta) }{P(y=0|X; \theta) }=\theta^TX$

Decision Boundary and Classifier

Therefore it is reasonable to make the following predication based the estimated probability:

When the probability of y =1 is greater than 0.5 then we can predict y = 1;
Else we predict y = 0.

From the property of Sigmoid function, we can get the equivalent Linear Decision Boundary or Linear Classifier is:

$\displaystyle \theta^TX=\theta_0+\theta_1x_1+\theta_1x_2 +...+ \theta_nx_n\ge 0$

Convex Cost Function

In the linear regression model, we use the Squared-Sum cost function $J(\theta)$ for the the linear hypothesis $H(\theta, X) = \theta^TX$ .

$\displaystyle J( \theta_0, \theta_1, \theta_2,....,\theta_n)=\frac{1}{2m}\sum_{i=1}^m (h(\theta, X_i) - y_i) ^2 =\frac{1}{2m}\sum_{i=1}^m (\theta^TX_i - y_i) ^2$

The Square-Sum cost function is convex.

However, for the logistics hypothesis here, the Square-Sum cost function $J(\theta)$ is no longer convex function at all now. It will not guarantee the global optimum. We need a different, convex Cost function which we can apply gradient descent.

New Cost Function

Intuitively, we can define

$\displaystyle \text{Cost}(h(\theta, X), y) = - \log P(Y=y|X;\theta), y = 0, or 1$

as the cost or error function for the data point $(X, y)$ .

Image [14]

That is,

$\displaystyle \text{Cost}(h(\theta, X),y)=\left\{ \begin{matrix}-\log h(\theta, X),& if y =1 \\-\log (1-h(\theta, X)),& if y=0\end{matrix}\right.$

Since y is always 0 or 1, we can rewrite the piece-wise cost function as

$\displaystyle \text{Cost}(h(\theta, X),y)= -y \log (h(\theta, X) ) - (1-y) \log (1-h(\theta, X))$

Therefore the logistic regression cost function is:

$\displaystyle J(\theta) = \frac{1}{m}\sum_{i=1}^m \text{Cost}(h(\theta, X_i),y_i)\\= -\frac{1}{m}\sum_{i=1}^m [y_i\log (h(\theta, X_i) ) - (1-y_i) \log (1-h(\theta, X_i))]$

where

$\displaystyle h(\theta,X)=\frac{1}{1+e^{-\theta^TX}}$

Good News: $J(\theta)$ is convex function of $\theta$ . We then can use the gradient descent method to minimize the cost function $\displaystyle \min_{\theta}J(\theta)$ :

Simultaneously update all $\theta_j, j=0,1,2,...,n$ :

$\displaystyle \theta_j :=\theta_j - \alpha \sum_{i=1}^{m} [h(\theta, X_i) - y_i]x_{ij}$

This equation is the same as the linear regression rule. The only difference is that our definition for the hypothesis has changed.

Multiclass classification problems

Given a training dataset with three classes C1, C2,. and C3, how do we get a regression learning algorithm to classify a new sample?

One vs. All Classification

Replicate or split the training set into three new training sets:
- TS1: Set all the C1 target value = 1, and all other target values = 0.
- TS2: Set all the C2 target value = 1, and all other target values = 0.
- TS3: Set all the C3 target value = 1, and all other target values = 0.
Use each of the new training set TS1, TS2, TS3 independently train the logistic regression classifier to get three hypothesis $h(\theta^{(1)}, X)$ , $h(\theta^{(2)}, X)$ , $h(\theta^{(3)}, X)$ .
For the new input X, pick the class that maximize the hypothesis ( probability) $h(\theta^{(k)}, X)$

Uncategorized

Linear Regression with Multiple Variables

August 15, 2014 lukelushu 1 Comment

Linear regression is a supervised learning algorithm and it attempts to model the relationship between two variables by fitting a linear equation to the training or observed data. It can be used tp solve the prediction or classification problems.

Problem Formulation

Let

$X=(x_0,x_1,x_2, ...., x_n ) \in R^{n+1}$ be an (n+1)-dimensional vertical vector, where we always have $x_0 = 1$ as the “bias”, and $x_1, x_2, ..., x_n$ are the n features (the n independent variables).

$y \in R^1$ be the dependent “target” variable.
$(X, y)$ is a single training example
$\{(X_i, y_i), i= 1,2,....,m\}$ the training set with m examples. The i-th sample is $X_i = (x_{i0}, x_{i1}, x_{i2}, ...,x_{in})^T$ , where $x_{ij}$ is the j-th feature value.
Hypothesis of the linear relationship $y = h(\theta, X)$ , where $\theta = (\theta_0,\theta_1,\theta_2, ...., \theta_n) \in R^{n+1}$ is the n+1 parameters to be determined, and

$h(\theta, X) = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + ....+ \theta_n x_n = \theta^TX$

The Cost Function is:

$\displaystyle J( \theta_0, \theta_1, \theta_2, ...., \theta_n) = \frac{1}{2m} \sum_{i=1}^m (h(\theta, X_i) - y_i) ^2$

Then the algorithm’s objective of to Minimize the cost function J() over the $\theta$ -parameter space. That is:

$\displaystyle \min_{\theta_0,\theta_1,...,\theta_n }J( \theta_0, \theta_1, \theta_2, ...., \theta_n)$

Gradient Descent

Gradient Descent is an optimization method that is used all over machine learning for minimization.

To Minimize cost function $J( \theta_0, \theta_1, \theta_2, ...., \theta_n)$ , do the following until convergence:

Simultaneously Update:

$\displaystyle \theta_j := \theta_j - \alpha \frac{\partial}{\partial \theta_j}J(\theta_0, \theta_1, \theta_2, ...., \theta_n), j= 0,1,2,...,n.$

where $\alpha$ is the learning rate.

Warning: If you implement the non-simultaneous update it’s not gradient descent, and will behave weirdly.

Linear Regression Algorithm

For the linear regression cost function

$\displaystyle J( \theta_0, \theta_1, \theta_2, ...., \theta_n) = \frac{1}{2m} \sum_{i=1}^m (h(\theta, X_i, - y_i ) ^2$

It is easy to get:

$\displaystyle \frac{\partial}{\partial \theta_j}J(\theta)=\frac{1}{m}\sum_{i=1}^m[h(\theta, X_i)-y_i]x_{ij},j=0,1,2,...,n.$

So we can use this to Simultaneously update

$\displaystyle \theta_j := \theta_j - \alpha\frac{1}{m}\sum_{i=1}^m[ h(\theta, X_i)-y_i]x_{ij}, j= 0,1,2,...,n.$

Feature Scaling

If you have a problem with multiple features, you should make sure those features have a similar scale, so that the gradient descent can converge more quickly. We need to rescale the features so the Contours become more like circles, and the algorithm is more effective.

Scaling Methods:

Max-Min Normalization: xi <– (xi – min) / (max – min)
Mean Normalization: xi <– (xi – mean)/max
Standardization: xi <– (xi – mean)/std

Learning Rate α

How to chose α? Make sure the gradient descent is working.
Plot min J(θ) vs. no of iterationsf gradient descent is working then J(θ) should decrease after every iteration
If you plot J(θ) vs iterations and see the value is increasing – means you probably need a smaller α
Use a smaller α. If α is small enough, J(θ) will decrease on every iteration
BUT, if α is too small then teh convergence is too slow
Typically
1. Try a range of alpha values
2. Plot J(θ) vs number of iterations for each version of alpha.
3. Go for roughly threefold increases: 0.001, 0.003, 0.01, 0.03. 0.1, 0.3

Least-squares Estimation and Normal Equation

In statistics, we have the below normal equation for the parameters estimation:

$\hat{\boldsymbol\beta} = (\mathbf{X}^{\rm T}\mathbf{X})^{-1} \mathbf{X}^{\rm T}\mathbf{y} = \big(\,{\textstyle\sum} \mathbf{x}_i \mathbf{x}^{\rm T}_i \,\big)^{-1} \big(\,{\textstyle\sum} \mathbf{x}_i y_i \,\big).$

where X is the design mX(n+1) matrix which contains all the training data features (including the the column bias). y is the column vector or mX1 matrix which is formed by the m target values from the training data.

Gradient Descent or Normal Equation

Gradient Descent

Need to chose learning rate
Needs many iterations – could make it slower
Works well even when n is massive (millions)
Better suited to big data
What is a big n though
100 or even a 1000 is still (relativity) small

Normal Equation

No need to chose a learning rate
No need to iterate, check for convergence etc.
Normal equation needs to compute the inverse of an nXn matrix (X’X).
- matrix inverse computing grows by O(n3 ) — so not great
Slow when n is large — Can be much slower

Polynomial Regression

By choosing appropriate features you can get different learning algorithms.

By performing appropriate features mapping, We can get polynomial regression for non-linear function from the Linear Regression developed above:

Polynomial Regression:

Hypothesis of polynomial relationship for the single variable x:

$h(\theta, x) = \theta_0 + \theta_1 x + \theta_2 x^2 + ....+ \theta_n x^n$

We can use the Features mapping: $x^i: \rightarrow x_i (i=1,2,...,n)$ to covert the Polynomial Regression into the Linear Regression problem with multiple variables

Machine Learning

Clustering: K-Means and K-Nearest Neighbor

August 13, 2014 lukelushu Leave a comment

K-Means and K-Nearest Neighbor (aka K-NN) are two commonly used clustering algorithms. They all automatically group the data into k-coherent clusters, but they are belong to two different learning categories:

K-Means — Unsupervised Learning: Learning from unlabeled data
K-NN — supervised Learning: Learning from labeled data

K-Means

Input:

K (the number of clusters in the data).
Training set: $\{X_i, i=1,2,..., N\}$ .

Algorithm:

Initialization: Randomly choose K points $\{C_k, k=1,2,...,K \}$ from the training set as the initial cluster centroids.
Repeat: {

a. Assign Cluster Step:

for each example $\{X_i \}$

Calculate the K-distances $||X_i - C_k||, k=1,2,...,K$ .

Set the class label $cl_i :=$ the index of k (from 1 to K) of the cluster centroids having the minimum distance ( $cl_i \in \{1,2,...,K\}$ ).

b. Move Centroids Step:

for $k = 1 \text{ to } K$ (for each class)

$C_k :=$ mean of the examples assigned to cluster k

} Until convergence, ie. there is no now centroids and classification

K-Means Optimization Objective

Let $\{C_k, k=1,2,...,K \}$ be the K centroids, $\{cl_i , i =1, 2,..., N \}$ be the index of cluster {1,2,…,K}. So the optimization objective of K-Means is:

$\displaystyle \min_{C_k, cl_i} J(C_1,C_2, ..., C_K, cl_1, cl_2, ..., cl_N) = \frac{1}{N} \sum_{i=1}^N||X_i - C(cl_i) ||^2$

where $C(cl_i)$ is the centroid to which the exsample $X_i$ has been assigned to.

Therefore, for the K-means algorithm,

Assign Cluster Step: Minimizing J(…) with respect to the cluster index $cl_i$ without changing the centroid $C_k$ .
Move Centroid Step: Minimizing J(…) with respect to the cluster centroid $C_k$ without changing the cluster index $cl_i$ .

How to Choose the Number K

Choosing K?

Not a great way to do this automatically
Normally use visualizations to do it manually

Elbow Method

Vary K and compute cost function J(…) for the K.
As K increases J(…) minimum value should decrease (i.e. you decrease the granularity so centroids can better optimize)
Plot this (K vs J())
Look for the “elbow” on the graph
Chose the “elbow” number of clusters
Not really that helpful. — If you get a nice plot this is a reasonable way of choosing K. However, normally you don’t get a a nice line -> no clear elbow on curve.

k-Nearest Neighbor:

Input:

K (the number of nearest neighbor chosen, typically small positive integer).
Training set with N samples and M known clusters (N>>M) : $\{(X_i, c_i) i=1,2,...,N\}$ . Where $c_i \in \{1, 2, ...,M\}$ .

Algorithm:

For a given new unlabeled sample,

Calculate its distances to all the training samples
Choose the K nearest samples based on the calculated distance
Count the vote for the chosen clusters.
Assign a cluster to the new unlabeled sample using the simple majority vote

Distance:

K-NN is a distance based learning, so choosing the an appropriate distance is very important. Below are the most used distance:

Let $X = (x_1, x_2, ..., x_n), Y = (y_1, y_2, ..., y_n)$ be two points in $R^2$ . Then Minkowski distance of order p is defined as

$D_p(X, Y) = \displaystyle \left ( \sum_{i=1}^n |x_i - y_i|^p \right ) ^{1/p}$

p = 1: Manhattan distance
p = 2: Euclidean distance
p = infinity: Infinity distance $D_{\\infty} = max \{ |x_i - y_i|\}$

It should also be noted that all three distance measures above are only valid for continuous variables. In instance of categorical variables the Hamming distance must be used:

$D_H(X, Y) = \displaystyle \sum_{i=1}^{n} |x_i - y_i|$

Standardized Distance

One major drawback in calculating distance measures directly from the training set is in the case where variables have different measurement scales or there is a mixture of numerical and categorical variables. For example, if one variable is based on annual income in dollars, and the other is based on age in years then income will have a much higher influence on the distance calculated. One solution is to standardize the training set as shown below:

$X_s = \displaystyle \frac{X-X_{min}}{X_{max} - X_{min}}$

	thx on The Trick of Retrieving the Sa…
	Jayron on The Trick of Retrieving the Sa…
	Abhirath Mahipal on Linear Regression with Multipl…
	zbra on The Trick of Retrieving the Sa…
	Bill Kuhn on The Trick of Retrieving the Sa…

Motivation

Linear Classifiers and Margin

How to Calculate the Margin Width

SVM – Optimization

1. How to Post Source Code — Code Snippet

2. How to Write Latex and Avoid the Not Parse Error

Data Profiling with Informatica IDQ

Problem

SAP ERP Metadat

Table Matadata Query:

Column Matadata Query:

Integrate the IDQ Data Profiling Result with the SAP Metadata

Metadata Integration Steps:

Regularization

Binary Class Problem

Logistics Hypothesis

Decision Boundary and Classifier

Convex Cost Function

Multiclass classification problems

One vs. All Classification

Problem Formulation

Gradient Descent

Linear Regression Algorithm

Feature Scaling

Scaling Methods:

Learning Rate α

Least-squares Estimation and Normal Equation

Gradient Descent or Normal Equation

Gradient Descent

Normal Equation

Polynomial Regression

Polynomial Regression:

K-Means

Input:

Algorithm:

K-Means Optimization Objective

How to Choose the Number K

Choosing K?

k-Nearest Neighbor:

Algorithm:

For a given new unlabeled sample,

Distance:

This blog will contain the technical notes for Oracle, Machine Learning, Quant tread, etc .